题解 P7478 StickSuger
贡献本题第一发 Python 题解。 截至发表之时是第一份有形象图片解释的题解。 可能是一种比较快的解法。  <p style="text-align: center;">( Python 区的第一份 AC 代码 )</p> ### 简化版题意描述 给您一个字符串 $s$,要求您给出最大的一个数对 $(i, j)$,使得交换中字符 $s[i], s[j]$ 之后的字符串比源字符串的字典序要大。如果没有符合要求的数对,输出 $-1$ 补充: > **简化版字典序概念**:对于两个相等长度的字符串 $s, t$,从头开始找,直到找到一个两字符串中字符不同的位置。如果 $s$ 这个位置的字符比 $t$ 的 ASCII 码要大,那么我们就说 $s$ 的字典序大于 $t$。 > > **关于 $(i, j)$ 数对的大小比较**:设两个数对 $(i_1, j_1)$, $(i_2, j_2)$,如果 $i_1 > i_2$,那么第一个数对比第二个数对大,如果二者的 $i$ 相同,那么就按照相同方式比较 $j$。 ### 思路 先说一下我们的思路:**从后往前找,直到找到一个极大点,然后在 “这个位置的前一个位置” 后面找到一个位置最大的比 “这个位置的前一个位置” 上的字符要大的字符,二者所在的位置构成的数对就是答案。** > **关于极大点的定义**:对于一个位置 $i$ 使得 $s[i] > s[i - 1]$ 并且 $s[i] > s[i + 1]$ 为什么要这么做? 我们不妨采用画图~~数形结合~~的技巧。 我们将随便一个字符串上的位置和该位置的 ASCII 码作为坐标点,连成一个平滑曲线。 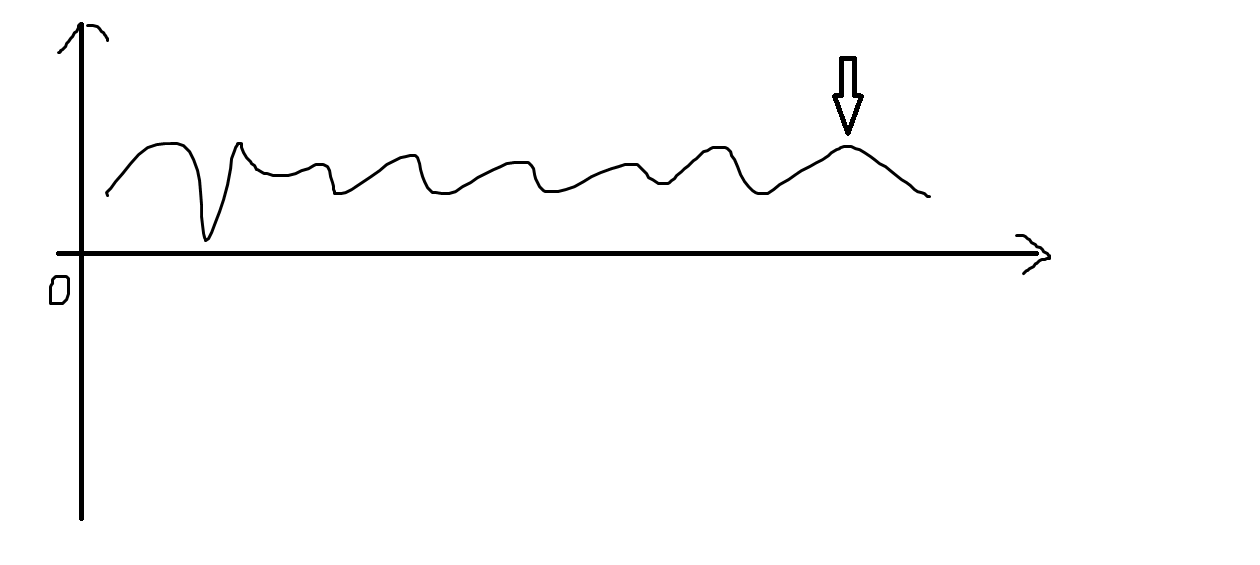 箭头标的位置就是最后一个极大点。 我们为什么要找到这个极大点? 答案其实很简单,从图像中可以看出,**这个极大点以后的字符一定保证越来越小**。 如果我们交换了他后面的两个字符,那么**字符串字典序势必会变小**。 所以我们找到这个极大点,以他左边的一个点作为 $i$。 这样无论如何,**$i$ 后面至少有一个一个字符要比 $s[i]$ 大**,而这个位置就是那个极大点。 我们确定了 $i$ 以后,就开始从后往前找 $j$,直到找到一个 $j$ 点的字符比 $i$ 点的大。 然后输出答案,一气呵成。 这就是 **“从后往前找,直到找到一个极大点,然后在 “这个位置的前一个位置” 后面找到一个位置最大的比 “这个位置的前一个位置” 上的字符要大的字符,二者所在的位置构成的数对就是答案。”** 的意义。 那么我们如何实现呢? 知道了原理以后实现就很简单了。我先把局部代码贴上来。 ```python # 定义字符串为 s, cur 为极大点位置,初始值为 -1 for i in range(n - 1, 0, -1): if s[i] > s[i - 1]: cur = i - 1; break ``` 很清晰,找到极大点并赋给 `cur`。 ```python # -1 就是没找到,是 cur 的初始值 if cur == -1: print("-1") else: for i in range(n - 1, cur, -1): if s[i] > s[cur]: print("%d %d" % (cur + 1, i + 1)); break ``` 找到极大点前面一个点,然后从后往前找 $j$ 至于为什么要输出 `(cur + 1, i + 1)`,自然是因为 Python 的字符串是以 $0$ 下标开始的。 ### 代码 (Python) ```python # !usr/bin/python3.7 def main(): n = int(input()) s = input() cur = -1 for i in range(n - 1, 0, -1): if s[i] > s[i - 1]: cur = i - 1; break if cur == -1: print("-1") else: for i in range(n - 1, cur, -1): if s[i] > s[cur]: print("%d %d" % (cur + 1, i + 1)); break return if __name__ == "__main__": main() ``` --- 其实赛时我写了一份 C 语言代码,但是没有什么特别之处,就在此处文章末尾贴出了。 赛时跑了 22ms,还是挺快的。 吸氧以后刷进最优解前六,应该还是比较不错的。  代码 (C 语言) ```c #include <stdio.h> int n, cur; char a[1000005]; int main() { scanf("%d", &n); scanf("%s", a + 1); for (int i = n; i >= 2; --i) if (a[i] > a[i - 1]) { cur = i - 1; break; } if (cur == 0) printf("-1\n"); else for (int i = n; i >= cur + 1; --i) if (a[i] > a[cur]) { printf("%d %d\n", cur, i); break; } return 0; } ```
<<< Return to archive list