题解 P6857 【梦中梦与不再有梦】
### Upd 2020 . 10 . 20 17 : 51 感谢 东北小蟹蟹 对于我的错误的指正QWQ  ## 背景 看到这个题的时候我想起了一笔画.... **对于每个桥梁 $e\text{{u,v}}$ ,它只能被经过一次,无论是正向经过还是反向经过。** 这不就是一个一笔画嘛.. 从一个点出发,一笔画出所有的边 ## 解法 所以我们按照一笔画的解法就可以了 如何可以得出一个一笔画? ------------ ~~众所周知~~, 当一个完全图的顶点为奇数个点时,那整个图就是一个一笔画图。 当一个完全图的顶点为偶数个点时,要保证整个图中只有两个点的度数为奇数。 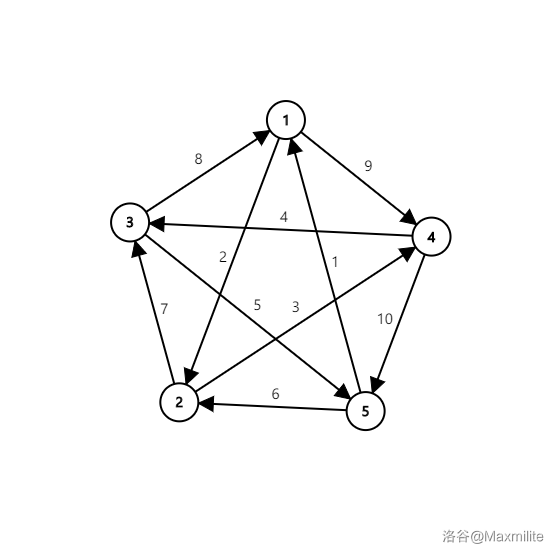 ##### (以一个顶点个数为奇数 $5$ 的完全图举例 该完全图可一笔完成) (度数指的是这个点连接的边的个数) (这里的完全图指的是通过图中所有边且每边仅通过一次通路) 所以我们的思路就很清晰了 #### **对于奇数顶点 直接输出完全图的总边数** 对于奇数 n,有完全图的总边数公式: $\dfrac{n(n - 1)}{2}$ #### **对于偶数顶点 稍微麻烦一点** 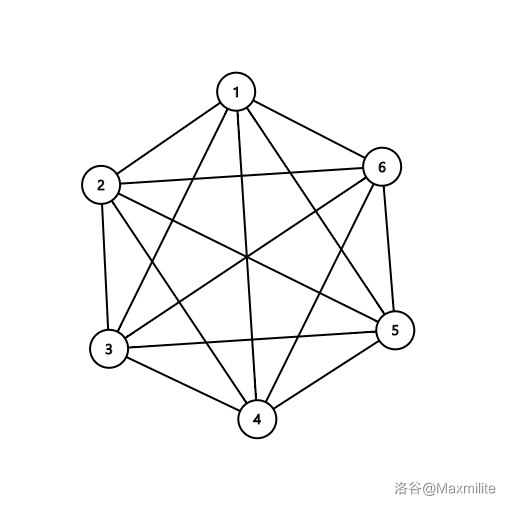 ##### (以一个顶点个数为偶数 $6$ 的完全图举例 这里全部的顶点度数都是奇数 $5$) 这里我的思路是: 对于偶数 $n$ 既然要保证只有两个点的度数为奇数 那么就要删除掉一些边来达成这一条件 而删除一条边会让两个顶点的度数由奇数变成偶数 所以公式就有了 有完全图的边数公式: $\dfrac{n(n - 1)}{2} - \dfrac{n - 2}{2}$ 删除边的个数由上面求得 使 $n - 2$ 个点的度数变成偶数 即可求得 ## AC 代码 ```cpp #include <stdio.h> int main() { long n, T, ans; scanf("%ld", &T); while (T--) { scanf("%ld", &n); if (n % 2) { ans = (n * (n - 1) / 2); printf("%ld\n", ans); } else { ans = (n * (n - 1) / 2) - ((n - 2) / 2); printf("%ld\n", ans); } } return 0; } ```
<<< Return to archive list